Introduction:

The slope of a line is a fundamental concept in mathematics and plays a crucial role in various fields such as physics, engineering, and economics. It represents the measure of how steep a line is, indicating the rate at which one variable changes concerning another. Whether you're dealing with linear equations, graphing, or analyzing data, understanding how to calculate the slope of a line is essential. In this article, we will explore the concept of slope, its significance, and the methods to calculate it.

Definition of Slope:

The slope of a line is defined as the ratio of the vertical change (rise) to the horizontal change (run) between any two points on the line. Mathematically, it is represented as:

Slope (m) = change in y / change in x = Δy/Δx

Here, Δy is the change in the vertical directions, and Δx is the change in the horizontal direction. The ratio Δy/Δx gives the average rate of change of the line.

You can use online calculator - rate of change calculator

Methods to Calculate Slope:

1.Using Coordinates:

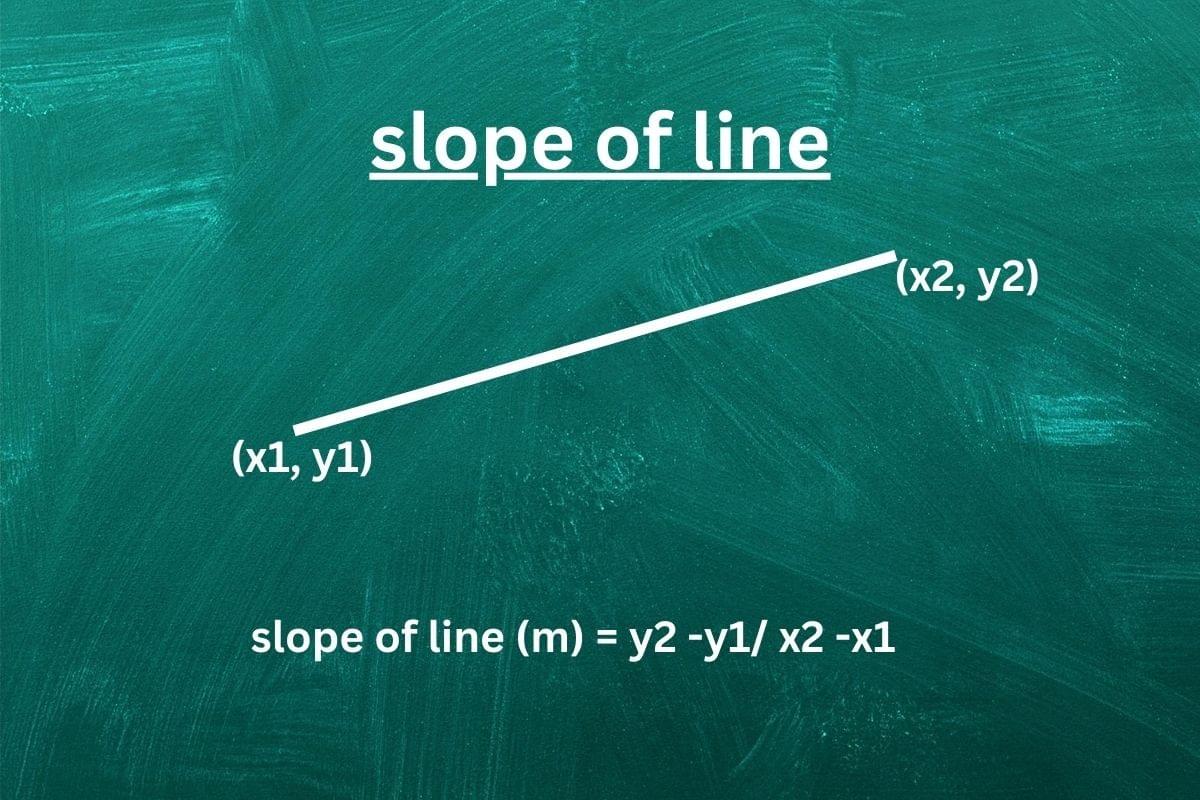
Given two points (x1, y1) and (x2, y2) on a line, the slope (m) can be calculated using formula:

M = y2-y1 /x2-x1

This method is straightforward and widely used when you have specific points on the line.

2.Graphical Method:

On a graph, the slope is visually represented by the steepness of the line. It is calculated by dividing the rise by the run between two points on the line. Count the number of units moved vertically (rise) and horizontally (run) to determine the slope.

3.Using the Slope-Intercept Form:

If the equation of the line is given in the slope-intercept form y = mx + b, where m is the slope, you can identify the slope directly from the equation. The coefficient of x represents the slope.

4.From a Table of Values:

If you have a table of values representing the relationship between

x and y, you can calculate the slope by choosing any two pairs of points and applying the slope formula.

M = change in y / change in x = y2 - y / x2 -x1

Significance of Slope:

• Rate of Change:
• The slope indicates how much one variable changes concerning another. In real-world scenarios, this can represent rates of speed, growth, or decline.
• Direction of the Line:
• The sign of the slope (+ or -) reveals the direction of the line on the coordinate plane. A positive slope indicates an upward direction, while a negative slope represents a downward direction.
• Interpretation in Context:
• In applications like economics and physics, the slope has meaningful interpretations. For instance, in a distance-time graph, the slope represents the speed of an object.

Conclusion

Calculating the slope of a line is a fundamental skill in mathematics and has widespread applications. Whether you're analyzing data, graphing equations, or interpreting real-world scenarios, understanding how to find the slope allows you to grasp the relationship between variables and make informed conclusions. By applying the various methods discussed in this article, you can confidently navigate the world of slopes and enhance your mathematical toolkit.